简单的Rosenblatt感知器与二维方差代价函数

文章发布时间:

文章总字数:
1.2k

预计阅读时间:
5 分钟

简单的Rosenblatt感知器

为了使得到的数据更加直观，我使用了python的matplotlib绘制图像

首先写一个可以获取散点的函数

1
2
3
4
5
6
7
import numpy as np

def get_beans(counts):
	xs = np.random.rand(counts)
	xs = np.sort(xs)
	ys = [1.2*x+np.random.rand()/10 for x in xs]
	return xs,ys

调用它并使其在坐标系中打印出来

1
2
3
4
5
6
7
8
9
10
11
import dataset
from matplotlib import pyplot as plt
xs,ys=dataset.get_beans(100)
print(xs)
print(ys)


plt.title("STF",fontsize=12)
plt.xlabel("B")
plt.ylabel("T")
plt.scatter(xs,ys)

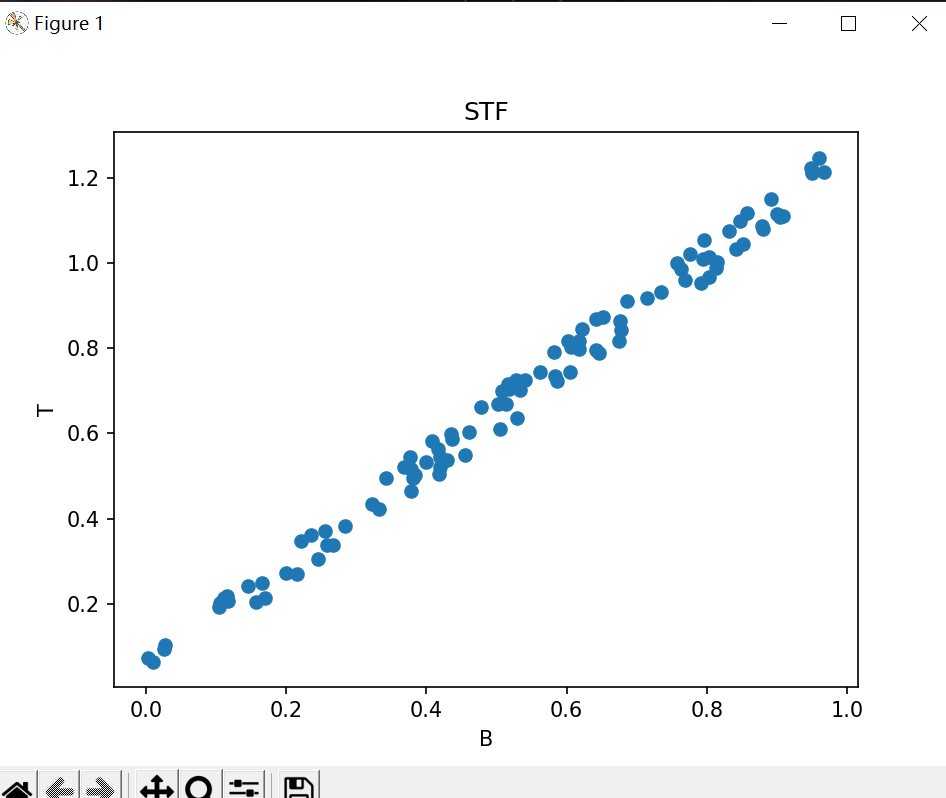
我们可以得到这样的一个图像

之后任意设定一个权重值w为0.1

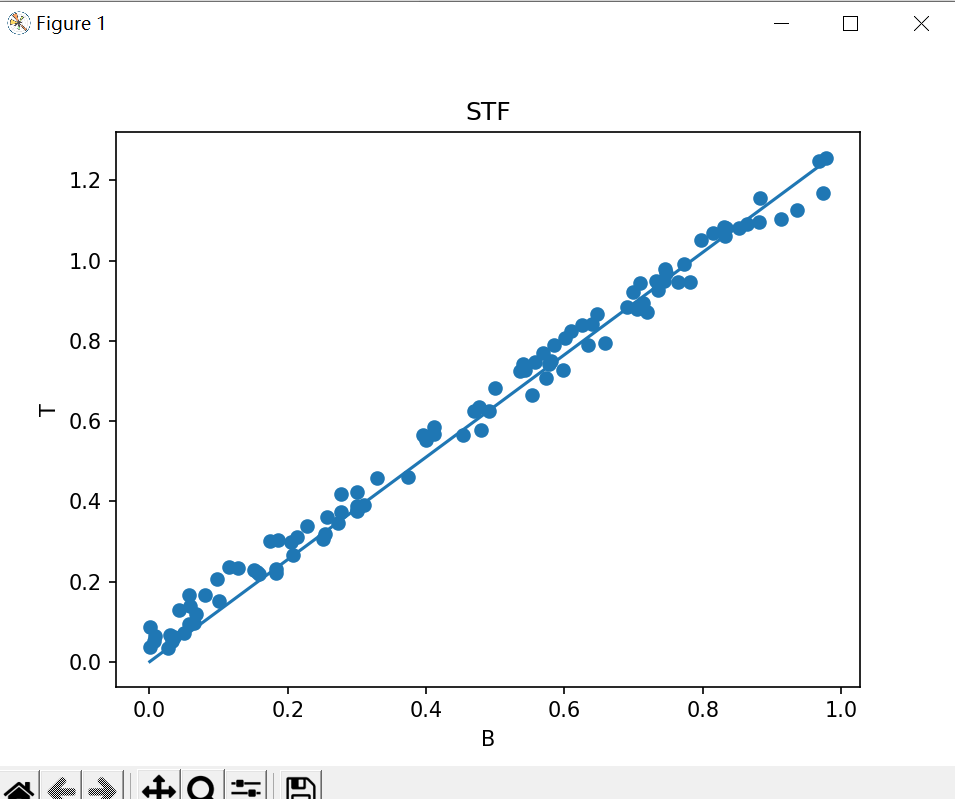
用标准答案减去该参数计算得到的结果得到一个误差，用原来的w加上alpha误差B（乘B是为了应对B为负数时，可能导致结果正好相反的情况，学习率alpha是为了控制调整的幅度，以免幅度过大错过最佳点）作为新的w，再一次进行运算。通过误差修正参数，这就是Rosenblatt感知器的学习过程。当然，这个公式在数学上是收敛的，Novikoff（1962）证明如果训练集是线性分隔的，那么感知器算法可以在有限次迭代后收敛，然而，如果训练集不是线性分隔的，那么这个算法则不能确保会收敛。以下代码简单的实现了 Rosenblatt感知器的学习过程 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import dataset
import numpy
from matplotlib import pyplot as plt
xs, ys = dataset.get_beans(100)
print(xs)
print(ys)


plt.title("STF", fontsize=12)
plt.xlabel("B")
plt.ylabel("T")
plt.scatter(xs, ys)

w = 0.5

for m in range(100):
	for i in range(100):
		x = xs[i]
		y = ys[i]
		y_pre = w * x
		e = y - y_pre
		alpha = 0.05
		w = w + alpha * e * x
y_pre = w * xs
print(y_pre)
plt.plot(xs, y_pre)
plt.show()

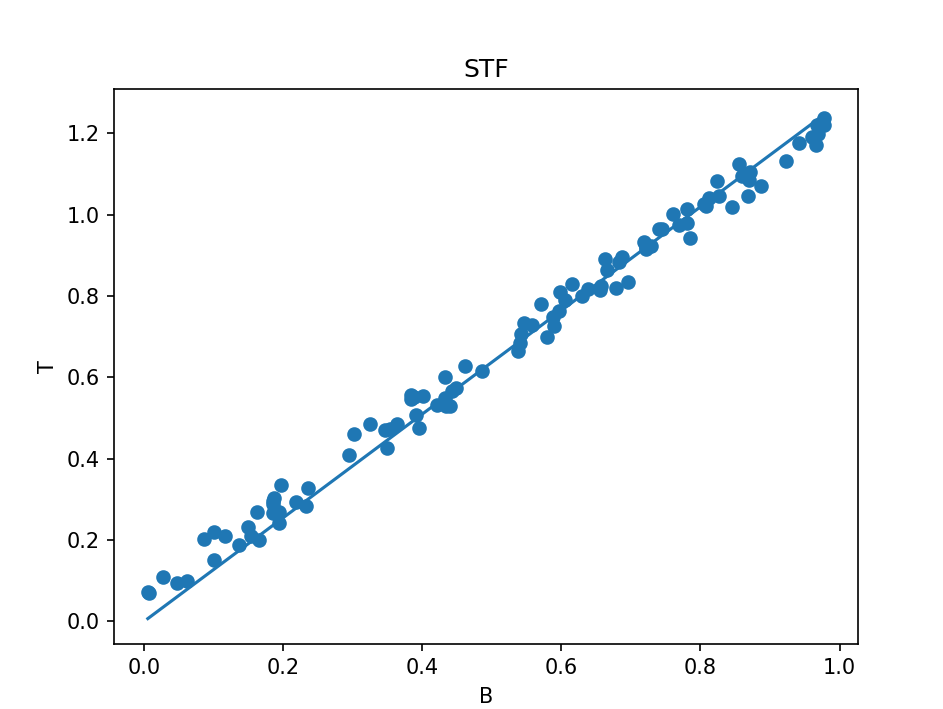
这样，运行后就可以得到一条与散点拟合的线

之后任意设定一个权重值w为0.1

用标准答案减去该参数计算得到的结果得到一个误差，用原来的w加上alpha误差B（乘B是为了应对B为负数时，可能导致结果正好相反的情况，学习率alpha是为了控制调整的幅度，以免幅度过大错过最佳点）作为新的w，再一次进行运算。通过误差修正参数，这就是Rosenblatt感知器的学习过程。当然，这个公式在数学上是收敛的，Novikoff（1962）证明如果训练集是线性分隔的，那么感知器算法可以在有限次迭代后收敛，然而，如果训练集不是线性分隔的，那么这个算法则不能确保会收敛。以下代码简单的实现了 Rosenblatt感知器的学习过程 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import dataset
import numpy
from matplotlib import pyplot as plt
xs, ys = dataset.get_beans(100)
print(xs)
print(ys)


plt.title("STF", fontsize=12)
plt.xlabel("B")
plt.ylabel("T")
plt.scatter(xs, ys)

w = 0.5

for m in range(100):
	for i in range(100):
		x = xs[i]
		y = ys[i]
		y_pre = w * x
		e = y - y_pre
		alpha = 0.05
		w = w + alpha * e * x
y_pre = w * xs
print(y_pre)
plt.plot(xs, y_pre)
plt.show()

这样，运行后就可以得到一条与散点拟合的线

方差代价函数

Rosenblatt感知器 其本身在现代神经网络研究中已经并不常用了，但我们依旧能从其中学习到参数的自适应调整是一个人工神经元的精髓。

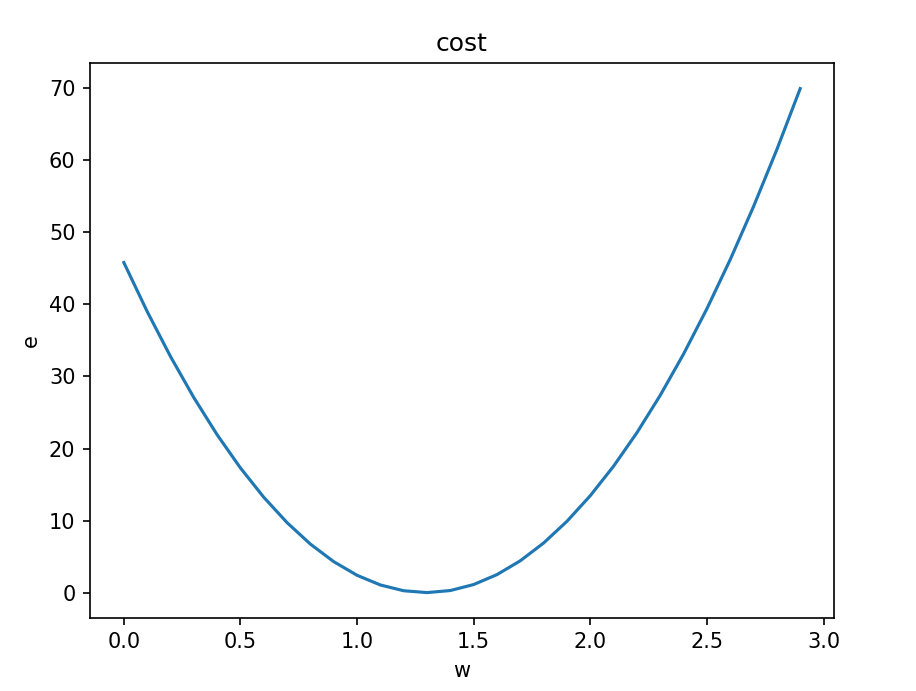
我们可以使用方差代价函数来评估误差从而达到参数的自适应调整。此时我们再次随便设定一个w，用统计到的数据去评估w的准确性，即回归分析。而我们可以使用最小二乘法来实现。我们将w作为自变量，误差e作为因变量，得到一个新的函数，即代价函数。他展现出当w取不同值时对于环境中问题数据进行预测时产生的误差e。因为他是一个二次函数，我们就可以利用它的最低点的w（此时e最小）带回预测函数，以此实现对参数w的自适应调整。

在之前代码的基础上进行修改，我们可以得到下面的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
import dataset
import matplotlib.pyplot as plt
import numpy as np
xs, ys = dataset.get_beans(100)


print(xs)
print(ys)


plt.title("STF", fontsize=12)
plt.xlabel("B")
plt.ylabel("T")
plt.scatter(xs, ys)

w = 0.1 # 可以任意
y_pre = w*xs
plt.plot(xs, y_pre)
plt.show()

es = (ys-y_pre)**2
 
sum_e = np.sum(es)

sum_e = (1/100)*sum_e

print(sum_e)

ws = np.arange(0,3,0.1)
# 从0到3每次增加0.1

es = []
for w in ws:
	y_pre = w*xs
	e = (1/100)*np.sum(ys-y_pre)**2
	es.append(e)


# 设定代价函数坐标系
plt.title("cost", fontsize=12)
plt.xlabel("w")
plt.ylabel("e")
plt.plot(ws,es)
plt.show()

w_min = np.sum(xs*ys)/np.sum(xs*xs)
print("eminw:"+str(w_min))
y_pre = w_min*xs
plt.title("STF", fontsize=12)
plt.xlabel("B")
plt.ylabel("T")
plt.scatter(xs, ys)


plt.plot(xs, y_pre)
plt.show()

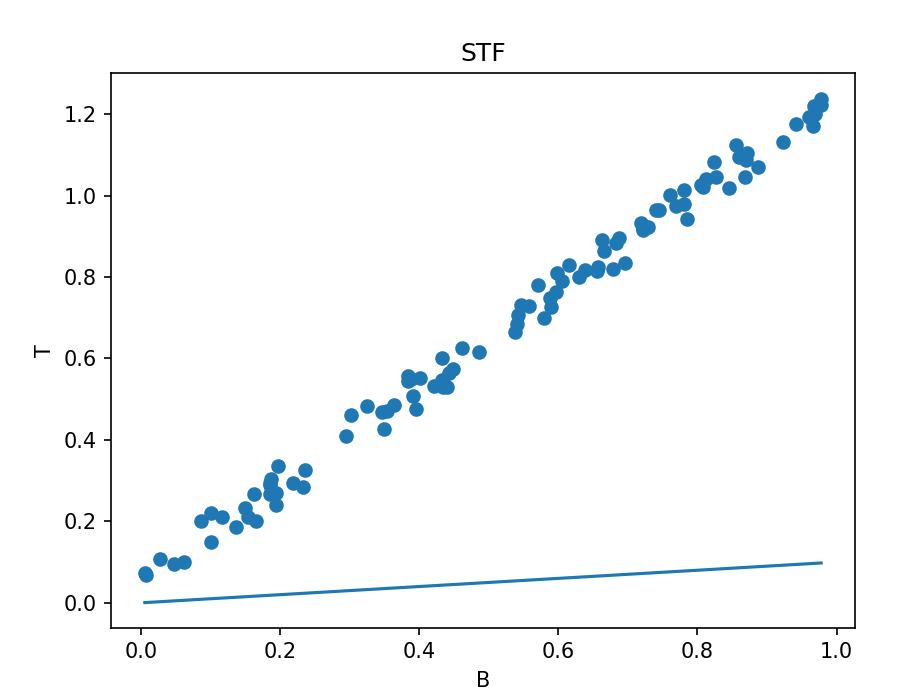
运行后得到三幅图

≡