简单的梯度下降算法实现

文章发布时间:

文章总字数:
942

预计阅读时间:
4 分钟

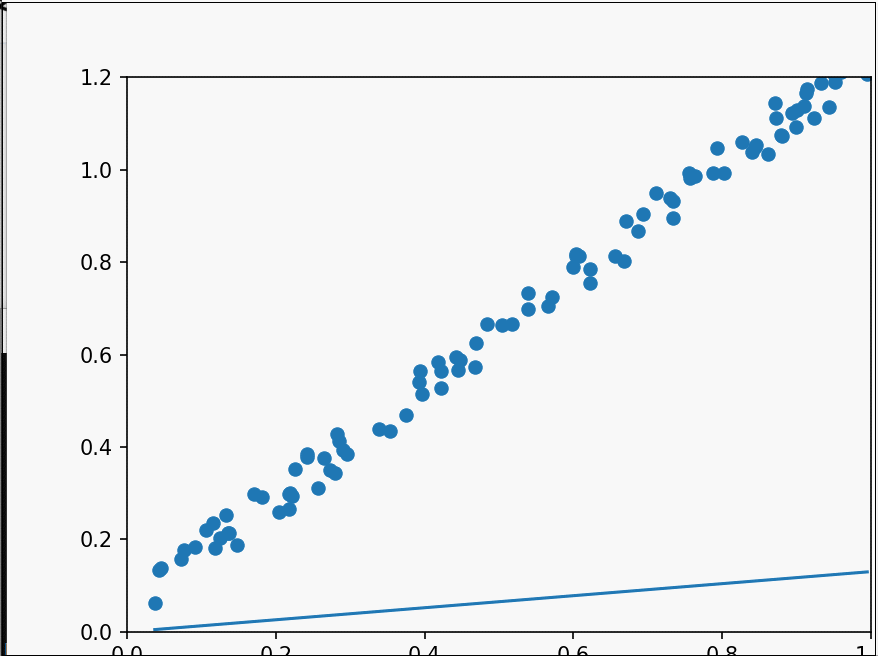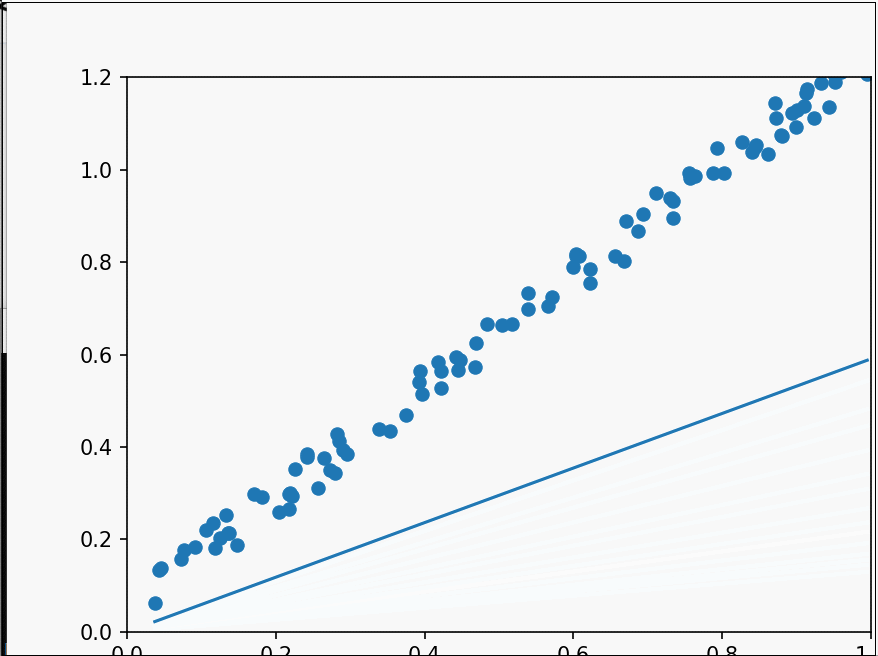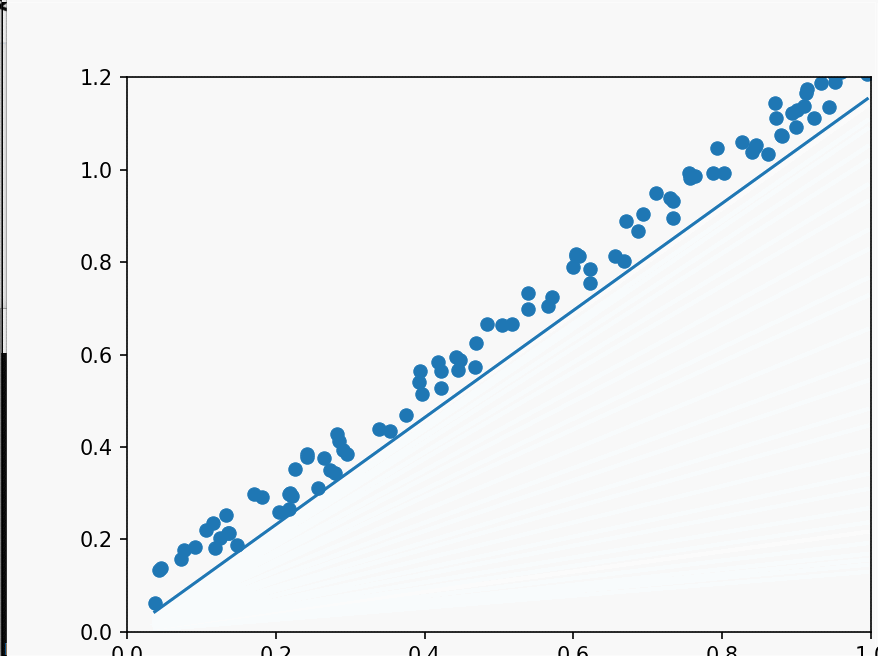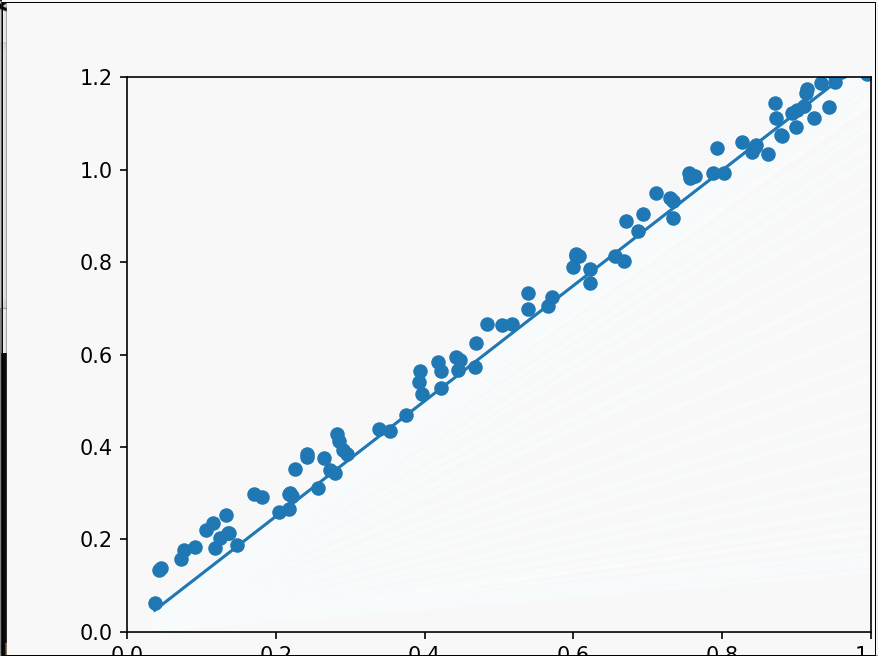
二维梯度下降

之前使用的算法是一次性计算出结果，在样本数量比较少的情况下还好，在样本较多的情况下，机器的算力可能不足以快速的计算出结果，这时候就需要使用梯度下降算法，我们先从简单的二维开始，即拟合y=wx。

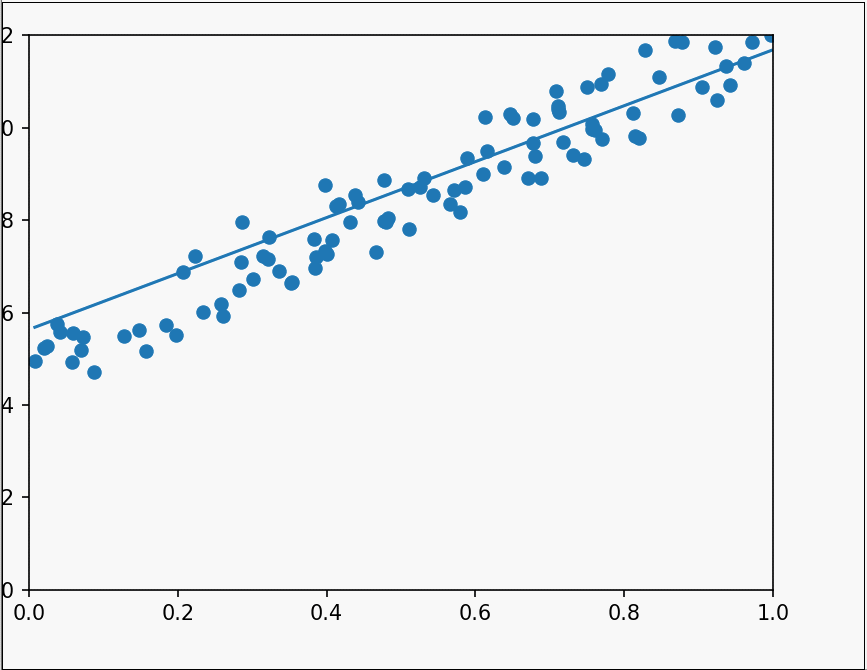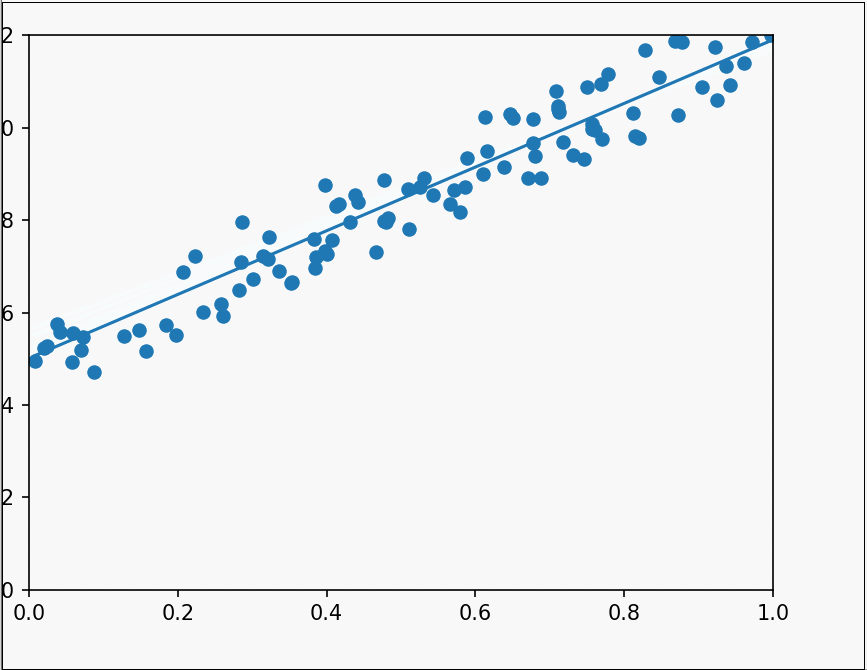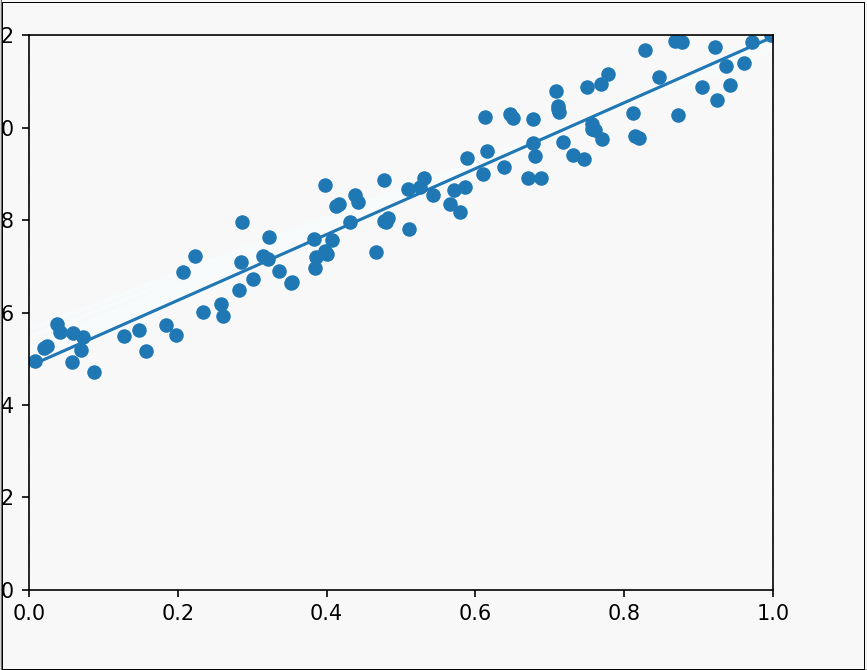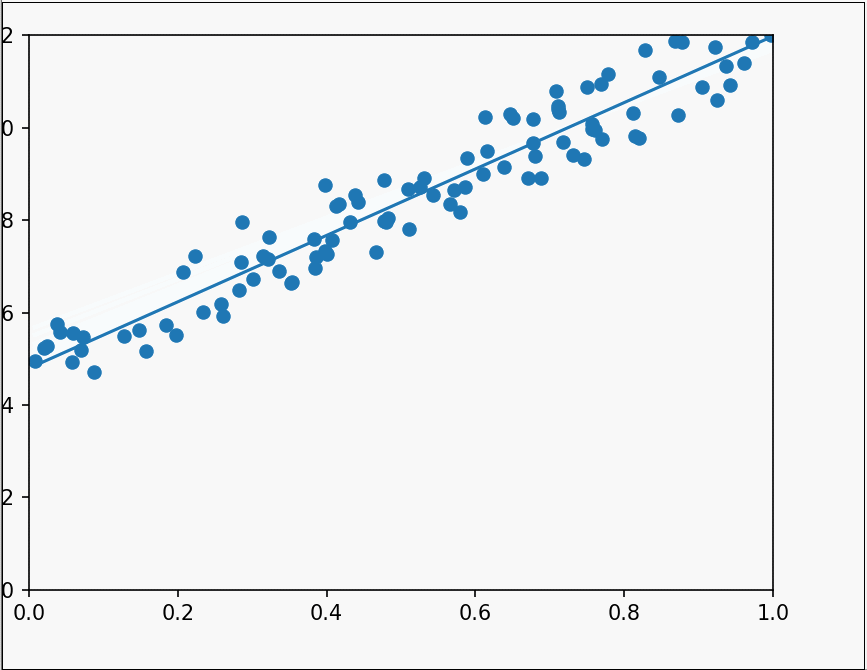
首先依旧是获取散点，绘制坐标系，预设一个w值为0.1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import dataset
import matplotlib.pyplot as plt
import numpy as np
xs, ys = dataset.get_beans(100)


print(xs)
print(ys)


plt.title("STF", fontsize=12)
plt.xlabel("B")
plt.ylabel("T")

plt.scatter(xs, ys)

w = 0.1
y_pre = w*xs
plt.plot(xs, y_pre)
plt.show()

这次写的是随机梯度下降算法，它的原理简单来说就是计算代价函数（w，e）在某一点的导数，用先前的w值减去学习率*斜率。因为在最低点右边时，斜率大于零，减去后向最低点靠拢，在左边时同理。学习率alpha的功能也是控制震荡幅度。这就是梯度下降。而随机指的是每次随机取样本中的一个数据验证拟合度，以避免在大量样本数时算力不足的情况

它的代码实现很简单，我在这里使用plt.clf()函数和plt.pause()函数相结合来实现动态图像，使拟合过程更加生动形象。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
for _ in range(100):
	for i in range(100):
		x = xs[i]
		y = ys[i]
		k = 2*(x**2)*w + (-2*x*y)
		alpha = 0.05
		w = w - alpha*k
		plt.clf()
		plt.scatter(xs, ys)
		y_pre = w*xs
		plt.xlim(0,1)
		plt.ylim(0,1.2)
		plt.plot(xs, y_pre)
		plt.pause(0.01)#暂停0.01秒

这样就实现了一个二维的随机梯度下降

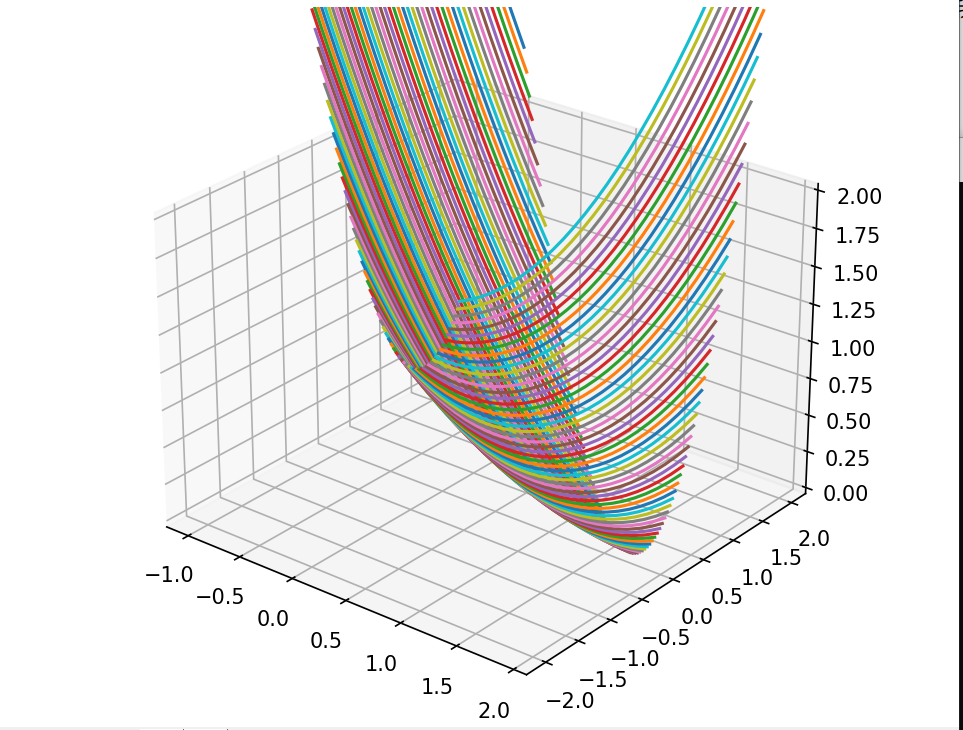
三维梯度下降

前面实现的二维梯度下降的算法比简单，但是不是所有的图像都会经过坐标原点，这时候w与e的函数便不再适用。完全的一次函数y=wx+b需要我们绘制w，e，b的三维代价函数，来求这个三维图像的最低点，这时候，我们便需要使用三维梯度下降。

首先我们先来绘制三维的代价函数图像，可以使用matplotlib中的Axed3D来实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import dataset
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

m=100
xs, ys = dataset.get_beans(m)

plt.title("STF", fontsize=12)
plt.xlabel("B")
plt.ylabel("T")
plt.xlim(0,1)
plt.ylim(0,1.5)

plt.scatter(xs, ys)

w = 0.1
b = 0.1
y_pre = w*xs + b

plt.plot(xs,y_pre)


plt.show()

fig = plt.figure()
ax = Axes3D(fig)
ax.set_zlim(0,2)

ws = np.arange(-1,2,0.1)
bs = np.arange(-2,2,0.04)

for b in bs:
	es = []
	for w in ws:
		y_pre = w*xs + b
		e = np.sum((ys-y_pre)**2)*(1/m)
		es.append(e)
	ax.plot(ws,es,b,zdir='y')
plt.show()

我们可以清晰地看到它有一个最低点，接下来我们就使用梯度下降算法得到它。

1
2
3
4
5
dw = 2*(x**2)*w + 2*x*b - 2*x*y
db = 2*b + 2*x*w -2*y
alpha = 0.05
w = w - alpha*dw
b = b - alpha*db

分别求得w和b方向上的斜率，把它们合到一起便实现了一次三维梯度下降

接下来就再用动态图像来观察三位梯度下降的过程，完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import dataset
import matplotlib.pyplot as plt
import numpy as np
xs, ys = dataset.get_beans(100)


print(xs)
print(ys)


plt.title("STF", fontsize=12)
plt.xlabel("B")
plt.ylabel("T")

plt.scatter(xs, ys)

w = 0.1
b = 0.1
y_pre = w*xs + b
plt.plot(xs, y_pre)
plt.show()

for _ in range(500):
	for i in range(100):
		x = xs[i]
		y = ys[i]
		dw = 2*(x**2)*w + 2*x*b - 2*x*y
		db = 2*b + 2*x*w -2*y
		alpha = 0.01
		w = w - alpha*dw
		b = b - alpha*db


	plt.clf()
	plt.scatter(xs, ys)
	y_pre = w*xs + b
	plt.xlim(0,1)
	plt.ylim(0,1.2)
	plt.plot(xs, y_pre)
	plt.pause(0.01)#暂停0.01秒

最后能得到这样的效果

≡