在现实中,判断一个物体,或者说对一个物体下定义,往往不能只从一个方面或两个方面观察。这时候,单个的Rosenblatt感知器已经无法胜任这样复杂的判断,是时候再增加一个神经元了。新增一个神经元,便增加了一个抽象的维度,每个维度通过不断地调整权重并进行激活,从而产生对输入的不同理解,最后再将这些抽象维度中的输出合并并降维得到最后的输出。而这些新添加的神经元,就被称之为隐藏层。
为了直观的看到效果,我还是使用了matplotlib进行绘图。这一次的w和b的值,我选择使用rand()函数生成随机数。并且为了之后的方便,将sigmoid函数(标准Logistic函数)和前向传播封装为两个函数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| import dataset
import matplotlib.pyplot as plt
import numpy as np
m = 100
xs, ys = dataset.get_beans(m)
plt.title("STF", fontsize=12)
plt.xlabel("B")
plt.ylabel("T")
plt.scatter(xs, ys)
def sigmoid(x):
return 1/(1+np.exp(-x))
#第一层
#第一个神经元
w11_1 = np.random.rand()
b1_1 = np.random.rand()
#第二个神经元
w12_1 = np.random.rand()
b2_1 = np.random.rand()
#第二层
w11_2 = np.random.rand()
w21_2 = np.random.rand()
b1_2 = np.random.rand()
#前向传播
def forward(xs):
#第一层第一个
z1_1 = w11_1*xs + b1_1
a1_1 = sigmoid(z1_1)
#第一层第二个
z2_1 = w12_1*xs + b2_1
a2_1 = sigmoid(z2_1)
#第二层(输出层)
z1_2 = w11_2*a1_1 + w21_2*a2_1 + b1_2
a1_2 = sigmoid(z1_2)
return a1_2,z1_2,a2_1,z2_1,a1_1,z1_1
|
这样准备工作就完成了,接下来就是繁琐的隐藏层求导进行反向传播的过程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| for _ in range(5000):
for i in range(100):
x = xs[i]
y = ys[i]
#先来一次前向传播
a1_2,z1_2,a2_1,z2_1,a1_1,z1_1 = forward(x)
#反向传播
#代价函数e
e = (y-a1_2)**2
deda1_2 = -2*(y - a1_2)
da1_2dz1_2 = a1_2*(1 - a1_2)
dz1_2dw11_2 = a1_1
dz1_2dw21_2 = a2_1
dedw11_2 = deda1_2*da1_2dz1_2*dz1_2dw11_2
dedw21_2 = deda1_2*da1_2dz1_2*dz1_2dw21_2
dz1_2db1_2 = 1
dedb1_2 = deda1_2*da1_2dz1_2*dz1_2db1_2
#隐藏层的第一个神经元
dz1_2da1_1 = w11_2
da1_1dz1_1 = a1_1*(1-a1_1)
dz1_1dw11_1 = x
dedw11_1 = deda1_2*da1_2dz1_2*dz1_2da1_1*da1_1dz1_1*dz1_1dw11_1
dz1_1db1_1 = 1
dedb1_1 = deda1_2*da1_2dz1_2*dz1_2da1_1*da1_1dz1_1*dz1_1db1_1
#隐藏层的第二个神经元
dz1_2da2_1 = w21_2
da2_1dz2_1 = a2_1*(1-a2_1)
dz2_1dw12_1 = x
dedw12_1 = deda1_2*da1_2dz1_2*dz1_2da2_1*da2_1dz2_1*dz2_1dw12_1
dz2_1db2_1 = 1
dedb2_1 = deda1_2*da1_2dz1_2*dz1_2da2_1*da2_1dz2_1*dz2_1db2_1
#梯度下降
alpha = 0.03
w11_2 = w11_2 - alpha*dedw11_2
w21_2 = w21_2 - alpha*dedw21_2
b1_2 = b1_2 - alpha*dedb1_2
w12_1 = w12_1 - alpha*dedw12_1
b2_1 = b2_1 - alpha*dedb2_1
w11_1 = w11_1 - alpha*dedw11_1
b1_1 = b1_1 - alpha*dedb1_1
|
经过漫长的求导与修改错误,最后再使用plt.clf()函数和plt.pause()函数相结合绘制动态图像,就得到了最终的结果。
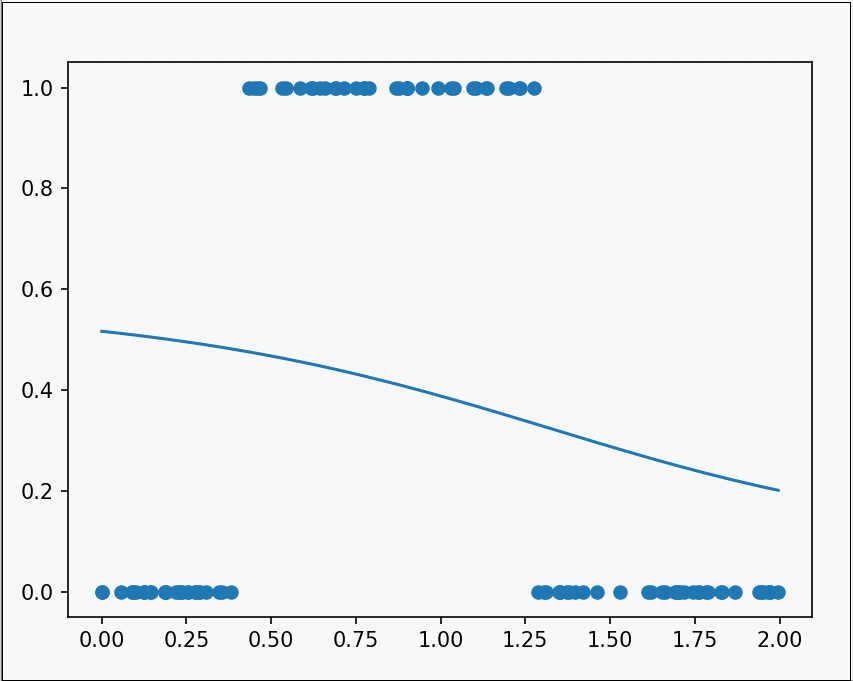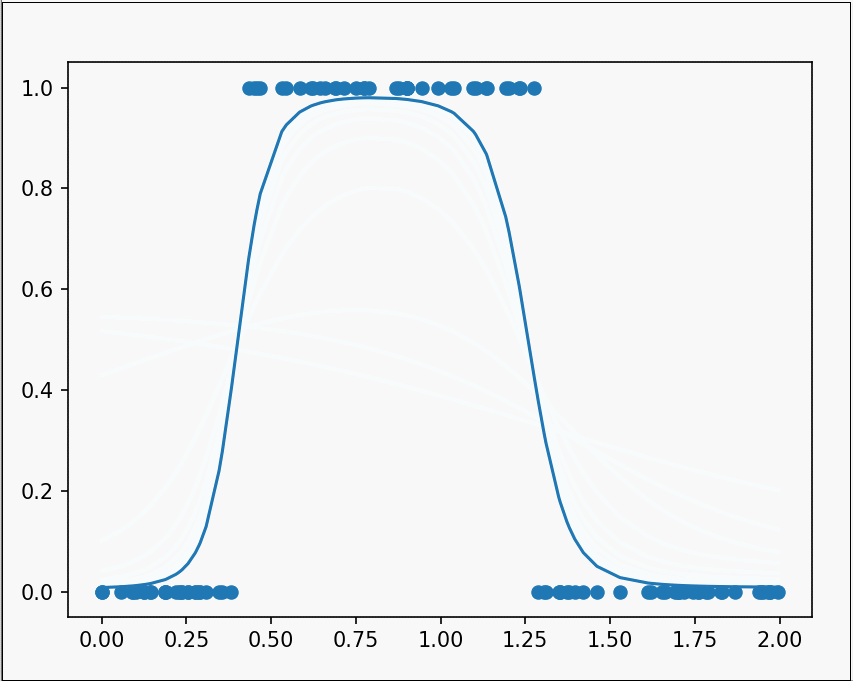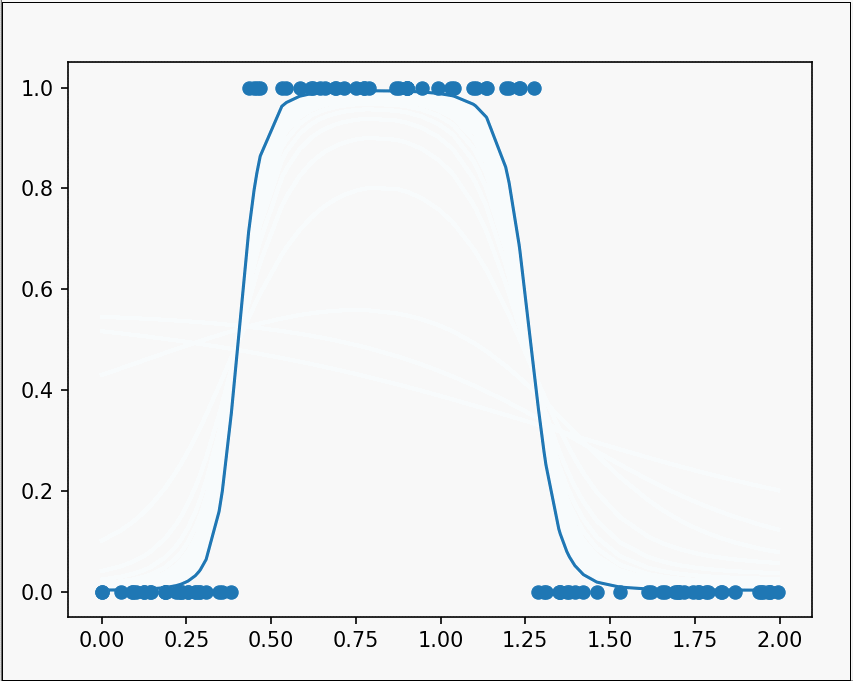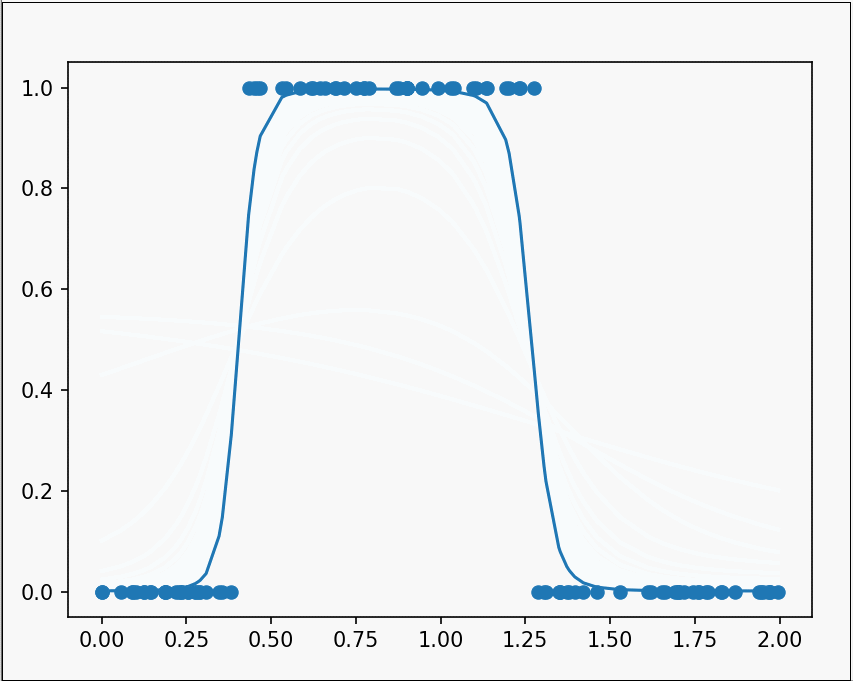
当隐藏层变得更多与更深,神经网络也会变得更加强大与智能。当我们设计出一个复杂程度恰当的神经网络,经过不断的训练过后,网络中的各个参数被调节成不同的值,而他们组成的整体,就可以近似出一个相当复杂的函数。
我们一般把隐藏层超过三层的网络称之为深度神经网络。隐藏层的神经元对样本的理解和提取的参数都太过微妙,我们能做的也只有设计一个网络,送入数据进行训练,如果效果好,那它就”起作用了“,效果不好就”没起作用“,只能再次调参,再来一次。这也是为什么深度学习被很多人戏称”炼丹“的原因。
