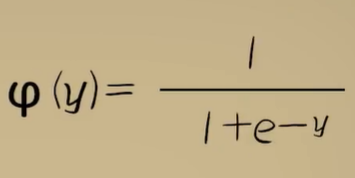之前对于一个函数的精确拟合的方式,对于一个智能体来说比较罕见,我们更多的是判断一个一个东西对,或者不对,最多再多一个不确定。这样的判断方式自然就和先前的拟合函数的方法相差甚远。为了达到这样的效果,我们便使用激活函数对之前的预测模型进行分类。而到此,我们才真正接触到了完整的Rosenblatt感知器模型。
为了进行分类,我们自然一开始就想到分段函数。但是这种函数在代码的层面上比较难以实现,所以,我们便引入了Logistic函数。
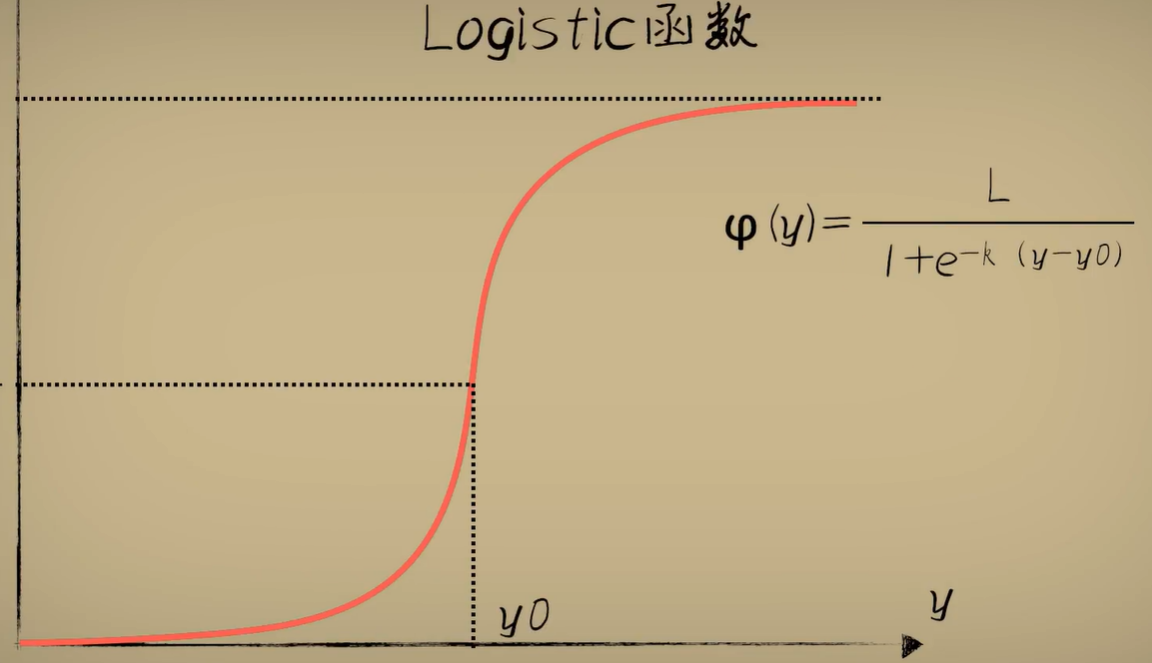
当然,我们一般取它的标准形式,即:
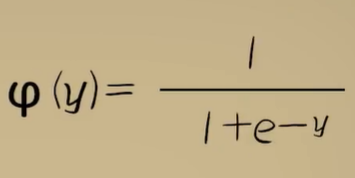
对于这样的函数我们可以使用nupmy库的exp()函数来实现:1/(1+np.exp(-y))。
这样我们便可以使用它来对预测结果进行分类了
利用复合函数求导的知识,对加入了激活函数的预测函数求偏导数。
1
2
3
4
5
6
7
| deda = -2*(y-a)
dadz = a*(1-a)
dzdw = x
dedw = deda*dadz*dzdw
dzdb = 1
dedb = deda*dadz*dzdb
|
再把这段代码加入之前的代码,在进行一些修改,我们可以得到最后的源码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| import dataset
import matplotlib.pyplot as plt
import numpy as np
xs, ys = dataset.get_beans(100)
print(xs)
print(ys)
plt.title("STF", fontsize=12)
plt.xlabel("B")
plt.ylabel("T")
plt.scatter(xs, ys)
w = 0.1
b = 0.1
y_pre = w*xs + b
plt.plot(xs, y_pre)
plt.show()
for _ in range(5000):
for i in range(100):
x = xs[i]
y = ys[i]
z = w*x + b
a = 1/(1+np.exp(-z))
e = (y-a)**2
deda = -2*(y-a)
dadz = a*(1-a)
dzdw = x
dedw = deda*dadz*dzdw
dzdb = 1
dedb = deda*dadz*dzdb
alpha = 0.05
w = w - alpha*dedw
b = b - alpha*dedb
if _%100 == 0:
plt.clf()
plt.scatter(xs, ys)
z = w*xs + b
a = 1/(1+np.exp(-z))
plt.xlim(0,1)
plt.ylim(0,1.2)
plt.plot(xs, a)
plt.pause(0.01)#暂停0.01秒
|
运行后可以观察到: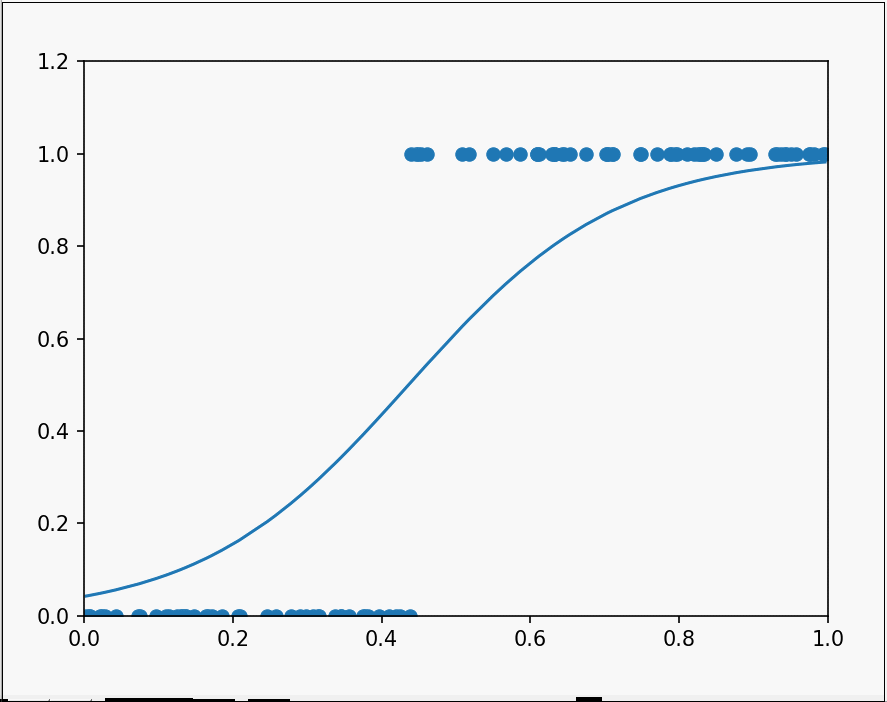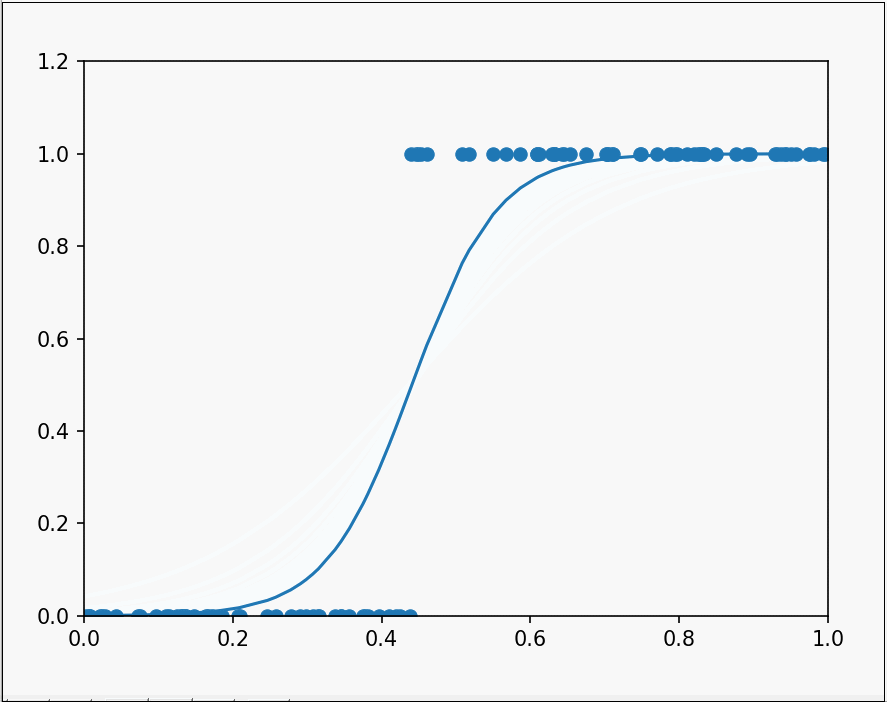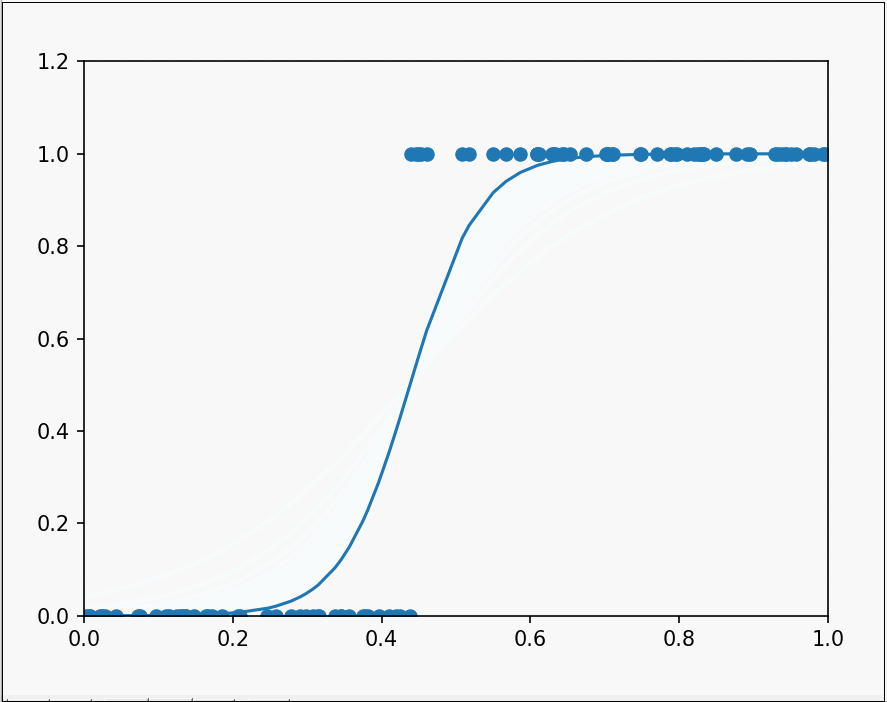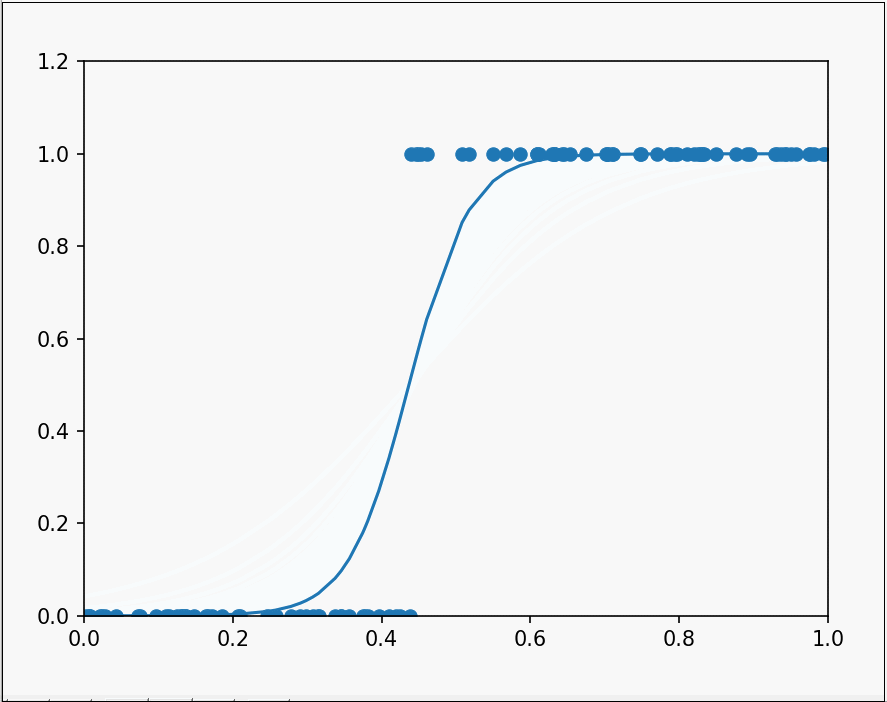
很好的对两类数据进行了分类。