高维空间——面对多个输入的问题

文章发布时间:

文章总字数:
738

预计阅读时间:
3 分钟

之前我已经讨论了从多个方面观察事物的问题，最后使用增加隐藏层来实现。但至始至终，我都只考虑了一个输入的情况，这也是之前的所有结果均可以在一个平面直角坐标系中画出。而现在，我们来考虑有多个输入的情况，这时，得到的结果便不再是一个平面图像了。

自然，为了更直观的看到最终拟合的状态，我们需要画一个图。我单独封装了一个plot_utils.py，这样直接import，在需要时就可以直接调用其中的函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

def show_scatter(xs,y):
	x = xs[:,0]
	z = xs[:,1]
	fig = plt.figure()
	ax = Axes3D(fig)
	ax.scatter(x, z, y)
	plt.show()

def show_surface(x,z,forward_propgation):
	x = np.arange(np.min(x),np.max(x),0.1)
	z = np.arange(np.min(z),np.max(z),0.1)
	x,z = np.meshgrid(x,z)
	y = forward_propgation(x,z)
	fig = plt.figure()
	ax = Axes3D(fig)
	ax.plot_surface(x, z, y, cmap='rainbow')
	plt.show()



def show_scatter_surface(xs,y,forward_propgation):
	x = xs[:,0]
	z = xs[:,1]
	fig = plt.figure()
	ax = Axes3D(fig)
	ax.scatter(x, z, y)

	x = np.arange(np.min(x),np.max(x),0.01)
	z = np.arange(np.min(z),np.max(z),0.01)
	x,z = np.meshgrid(x,z)
	y = forward_propgation(x,z)
	
	ax.plot_surface(x, z, y, cmap='rainbow')
	plt.show()

而这次，为了展现多个输入的情况，产生数据集的函数也有所不同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np

def get_beans(counts):
	xs = np.random.rand(counts,2)*2
	ys = np.zeros(counts)
	for i in range(counts):
		x = xs[i]
		if (x[0]-0.5*x[1]-0.1)>0:
			ys[i] = 1
	return xs,ys

def get_beans2(counts):
	xs = np.random.rand(counts,2)*2
	ys = np.zeros(counts)
	for i in range(counts):
		x = xs[i]
		if (np.power(x[0]-1,2)+np.power(x[1]-0.3,2))<0.5:
			ys[i] = 1


	return xs,ys

它会产生一个两列的数组。可以使用numpy库的特性分割开得到两组输入。

1
2
x1s = xs[:,0]#切割第0列形成一个新的数组
x2s = xs[:,1]

再将前向传播封装为一个函数：

1
2
3
4
def forward(x1s,x2s):
	z = w1*x1s + w2*x2s + b
	a = 1/(1+np.exp(-z))
	return a

最后，依旧利用反向传播与梯度下降算法进行学习拟合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
for _ in range(500):
	for i in range(m):
		x = xs[i]
		y = ys[i]
		x1 = x[0]
		x2 = x[1]

		a = forward(x1,x2)

		e = (y-a)**2

		deda = -2*(y-a)
		dadz = a*(1-a)
		dzdw1 = x1
		dzdw2 = x2
		dzdb = 1

		dedw1 = deda*dadz*dzdw1
		dedw2 = deda*dadz*dzdw2
		dedb = deda*dadz*dzdb

		alpha = 0.01
		w1 = w1 - alpha*dedw1
		w2 = w2 - alpha*dedw2
		b = b - alpha*dedb

最后我们可以得到这样的结果：

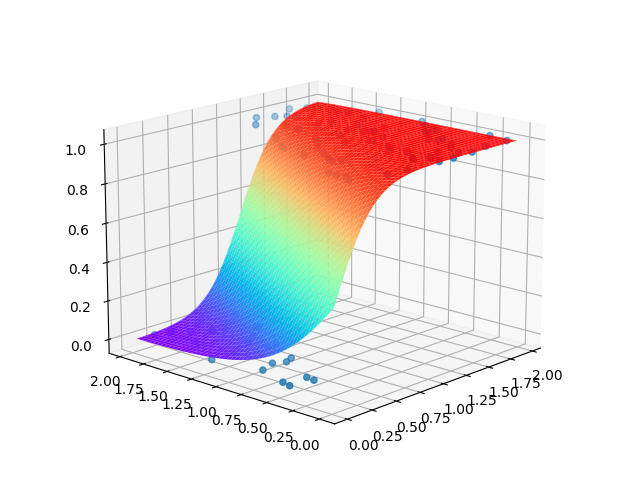
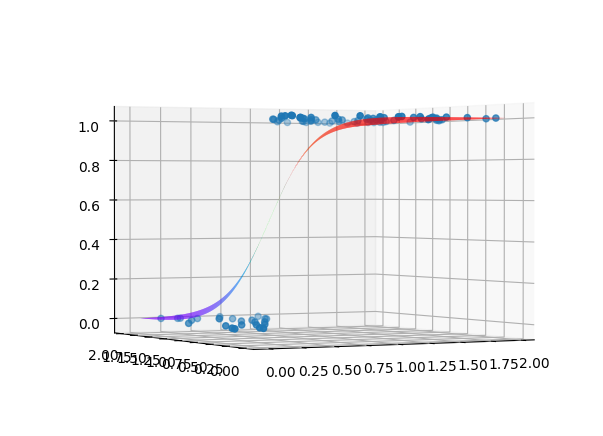
如果我们从另一个角度来看的话，它就和添加了激活函数后的最简单的Rosenblatt感知器模型得到的结果类似：

输入数据的增加会导致维度增加，但最为三维生物我们无法具象化三维以上的模型，但对于计算机来说，增加一个输入就是增加一维数组，这样高维空间的学习与计算对他来说也可以实现