数组的利用与初识Keras

文章发布时间:

文章总字数:
702

预计阅读时间:
3 分钟

在之前的学习中我一直使用的是方程的形式进行前向传播梯度下降与反向传播。然而随着输入参数与隐藏层的增多，方程形式似乎不再能胜任如此复杂的工作，这时候就需要引入另一个数学工具——矩阵。

numpy库是一个强大的数学计算库，使用它可以让矩阵的计算变得简单许多。

这是利用方程的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
w1 = 0.1
w2 = 0.1
b = 0.1

x1s = xs[:,0]#切割第0列形成一个新的数组
x2s = xs[:,1]

def forward(x1s,x2s):
	z = w1*x1s + w2*x2s + b
	a = 1/(1+np.exp(-z))
	return a
plot_utils.show_scatter_surface(xs,ys,forward)

for _ in range(500):
	for i in range(m):
		x = xs[i]
		y = ys[i]
		x1 = x[0]
		x2 = x[1]

		a = forward(x1,x2)

		e = (y-a)**2

		deda = -2*(y-a)
		dadz = a*(1-a)
		dzdw1 = x1
		dzdw2 = x2
		dzdb = 1

		dedw1 = deda*dadz*dzdw1
		dedw2 = deda*dadz*dzdw2
		dedb = deda*dadz*dzdb

		alpha = 0.01
		w1 = w1 - alpha*dedw1
		w2 = w2 - alpha*dedw2
		b = b - alpha*dedb

这是利用数组的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
W = np.array([0.1, 0.1])
B = np.array([0.1])



def forward(X):
	Z = X.dot(W.T) + B
	A = 1/(1+np.exp(-Z))
	return A
plot_utils.show_scatter_surface(X,Y,forward)

for _ in range(500):
	for i in range(m):
		Xi = X[i]
		Yi = Y[i]

		A = forward(Xi)

		E = (Yi-A)**2

		dEdA = -2*(Yi-A)
		dAdZ = A*(1-A)
		dZdW = Xi
		dZdB = 1

		dEdW = dEdA*dAdZ*dZdW
		dEdB = dEdA*dAdZ*dZdB

		alpha = 0.01
		W = W - alpha*dEdW
		B = B - alpha*dEdB

可以很直观的发现，使用数组（矩阵）时，代码量会少很多。并且面对越多的输入与隐藏层时，它的优势就会越明显。

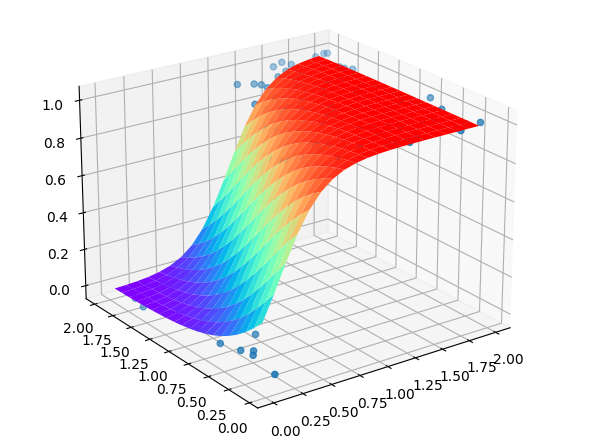
当然，它的拟合度也非常的好。

但是，在面对更加复杂的机器学习，比如卷积神经网络，使用这种编写底层代码的方式将会是个大工程。这时候，Keras就自然而然的进入了我的视野，正如它官网上那样：你恰好发现了Keras

现在，是时候走出对神经网络底层知识的学习，开始进入应用层的大门了。

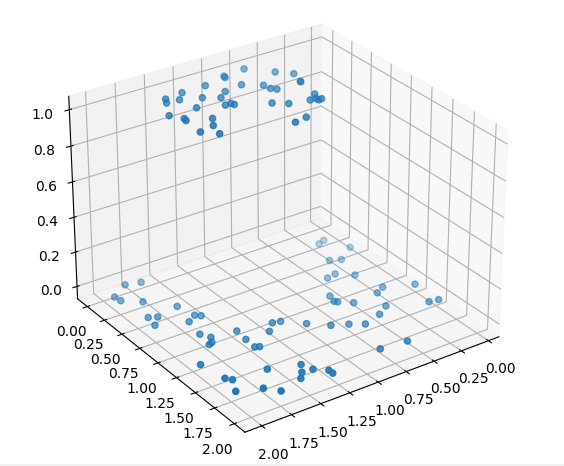
为了展现出Keras相较于手撸底层代码的优势，我使用了新的数据集

想要拟合这个数据集无疑会很繁琐，相较于上一个，它又增加了新的隐藏层，这样反向传播的求导过程将十分复杂，但使用Keras后，一切都简单了起来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import dataset
import numpy as np
import plot_utils
from keras.models import Sequential 
from keras.layers import Dense 
from tensorflow.keras.optimizers import SGD

m = 100
X, Y = dataset.get_beans4(m)
plot_utils.show_scatter(X,Y)

model = Sequential()
model.add(Dense(units=2, activation='sigmoid', input_dim=2))
model.add(Dense(units=1, activation='sigmoid',))

model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.05), metrics=['accuracy'])

model.fit(X, Y, epochs=5000, batch_size=10)

pres = model.predict(X)

plot_utils.show_scatter_surface(X, Y, model)

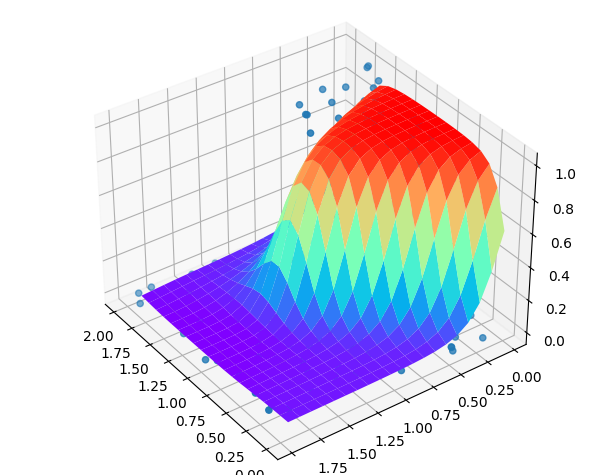
只需要小小的改一个数字就能增加隐藏层，这实在是太方便了。

效果也是非常的好