深度学习

深度学习，就是不断增加一个神经网络的隐藏层神经元，让输入的数据被这些神经元不断地抽象和理解，最后得到一个具有泛化能力的预测网络模型。而我们一般把隐藏层超过三层的神经网络称为“深度神经网络”。

我们很难用精确的数学手段去分析网络中的每一个神经元在想什么，我们能做的也就只有对学习率，激活函数，神经元数量等等方面进行更改，并送入数据进行训练，期待最后的结果。

想直观的体验这样的过程tensorflow游乐场是个很好的网站（https://playground.tensorflow.org）

接下来，我就使用Keras来实现一个简单的深度学习。

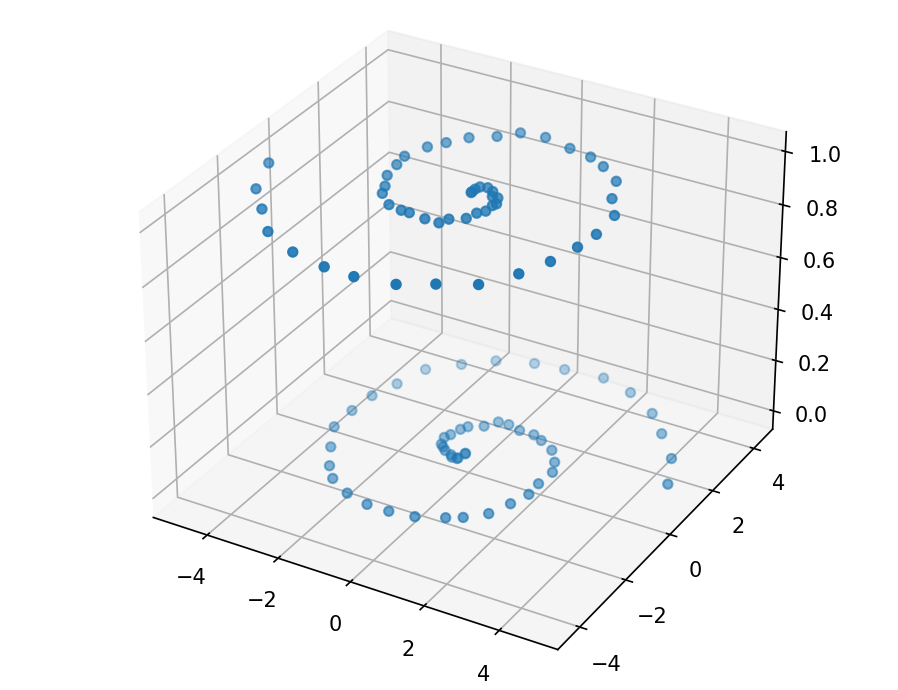
这次的散点图就变得更加复杂。

上下螺旋型的分布使得之前写过的所有模型都不再适合，这时候Keras的强大与便捷便体现了出来。只需要调一调参数，增加隐藏层数量，一个更加强的深度神经网络便形成了。

import dataset
import numpy as np
import plot_utils
from keras.models import Sequential 
from keras.layers import Dense 
from tensorflow.keras.optimizers import SGD

m = 100
X, Y = dataset.get_beans(m)
plot_utils.show_scatter(X,Y)

model = Sequential()
model.add(Dense(units=8, activation='relu', input_dim=2))
model.add(Dense(units=8, activation='relu',))
model.add(Dense(units=8, activation='relu',))
model.add(Dense(units=1, activation='sigmoid',))

model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.05), metrics=['accuracy'])

model.fit(X, Y, epochs=5000, batch_size=10)

pres = model.predict(X)

plot_utils.show_scatter_surface(X, Y, model)

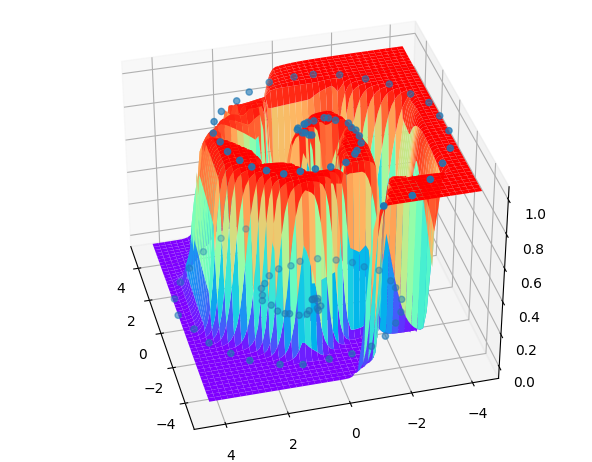
甚至不需要太多代码就能很好的拟合

卷积神经网络

在机器学习，神经网络领域，有一个应用层面上的经典的“hello world”。那就是手写体识别。因为它场景简单明确，更有经典的数据集mnist。

mnist数据集里是28*28像素的灰度图，用0到255来代表颜色的深浅。我们要怎样将一张图片送入神经网络进行学习呢？没错，我们把这些像素看成数字就好，这将形成一个最小值为0，最大值为255的(28,28)的矩阵，自然就可以送入学习了。

但是，如果使用全连接神经网络，即使把网络堆叠的越来越深，添加更多的隐藏层，用尽防止过拟合的方法，但泛化能力依旧不尽人意。在深度学习巨头Lecun整理的数据中，效果最好的全连接神经网络是2010年的一个6层的网络，规模已经达到了惊人的2500-2000-1500-1000-500-10，作者也毫不避讳的说到，他们就是硬算，他们有强大的显卡。

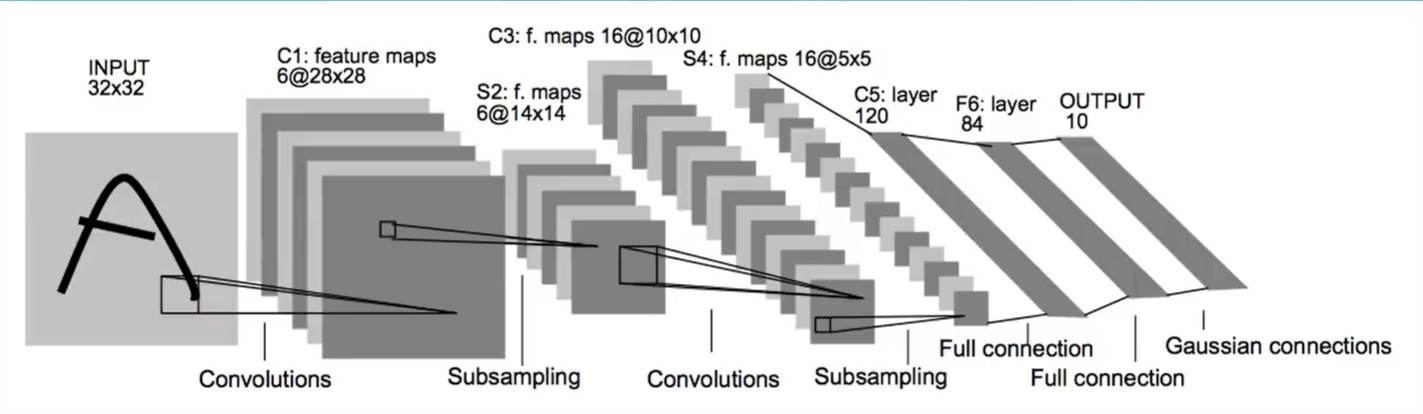
但对于卷积神经网络，即使是早在1998年提出的LeNet-5也比6层的全连接神经网络准确率更高。接下来我就用mnist数据集复现一下这个经典的卷积神经网络。

为了体现卷积神经网络的优势，我先用全连接神经网络搭建了一个模型。

from keras.datasets import mnist
import numpy as np
from keras.models import Sequential 
from keras.layers import Dense 
from tensorflow.keras.optimizers import SGD
import matplotlib.pyplot as plt
from tensorflow.keras.utils import to_categorical

(X_train, Y_train), (X_test, Y_test) = mnist.load_data() #均为numpy的ndarray类型

print("X_train.shape:"+str(X_train.shape))
print("Y_train.shape:"+str(Y_train.shape))
print("X_test.shape:"+str(X_test.shape))
print("Y_test.shape:"+str(Y_test.shape))

print(Y_train[0])
plt.imshow(X_train[0], cmap='gray')
plt.show()

X_train = X_train.reshape(60000,784)/255.0
X_test = X_test.reshape(10000,784)/255.0

Y_train = to_categorical(Y_train,10)
Y_test = to_categorical(Y_test,10)

model = Sequential()
model.add(Dense(units=256, activation='relu', input_dim=784))
model.add(Dense(units=256, activation='relu',))
model.add(Dense(units=256, activation='relu',))
model.add(Dense(units=10, activation='softmax',))

model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.05), metrics=['accuracy'])

model.fit(X_train, Y_train, epochs=5000, batch_size=2048)

pres = model.predict(X)

plot_utils.show_scatter_surface(X, Y, model)

这是一个256-256-256-10的模型。因为使用的是全连接层，所以我使用reshape()函数将600002828和100002828改成了60000784和10000784。又在 X_train 和 X_test 的值后/255进行归一化操作，将激活函数改为了更加适合多分类的softmax。运行得到的结果是这样的：

接下来就是复现 LeNet-5 卷积神经网络了

由架构图可以看到，在第一个卷积层，3232的图片被卷成了6个2828的，当然卷积核就是6个55的，步长为1。但由于mnist数据集本身就是2828的图片，所以实现时会有行一些改变。

model.add(Conv2D(filters=6, kernel_size=(5,5), strides=(1,1), input_shape=(28, 28, 1), padding='valid', activation='relu'))

之后是第一个池化层， LeNet-5使用的是2*2的平均池化。

model.add(AveragePooling2D(pool_size=(2,2)))

之后是第二个卷积层。它使用16个5*5的卷积核

model.add(Conv2D(filters=16, kernel_size=(5,5), strides=(1,1), padding='valid', activation='relu'))

之后是第二个相同的池化层。我们需要把最后这个池化层的输出平铺成一个数组。使用Keras的Flatten实现

model.add(Flatten())

后面的就是全连接层了。由架构图可以看到，最后是个120-84-10的全连接层

model.add(Dense(units=120, activation='relu'))
model.add(Dense(units=84, activation='relu'))
model.add(Dense(units=10, activation='softmax'))

这样， LeNet-5 网络就搭建好了。之后将mnist数据集送入训练并评估

model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.05), metrics=['accuracy'])
model.fit(X_train, Y_train, epochs=5000, batch_size=2048)

pres = model.predict(X)
plot_utils.show_scatter_surface(X, Y, model)

最后得到这样的结果

很明显可以看出是比全连接神经网络更好的。